Revolutionizing Geometry: Discover the Deep Insights into Cohomology Rings of Character Varieties
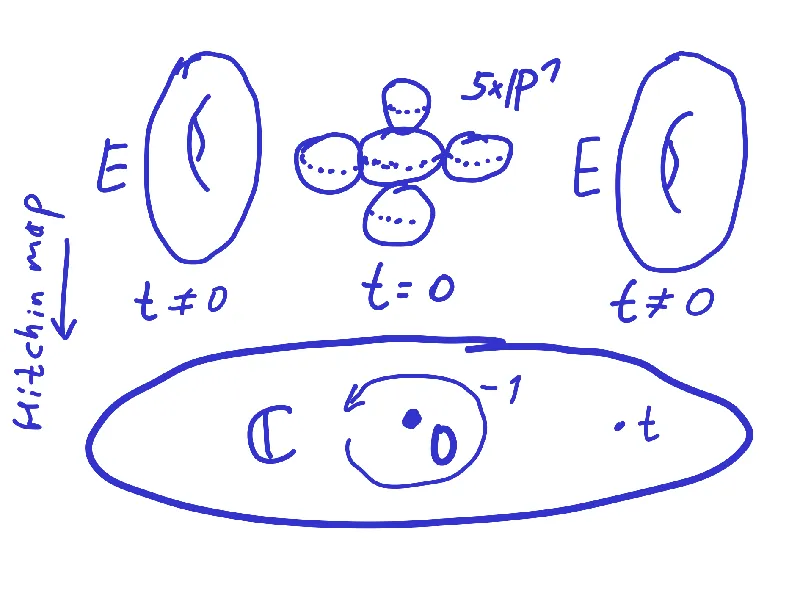
In a groundbreaking presentation, Anton Mellit unveils significant advancements in the study of cohomology rings of character varieties, particularly focusing on Riemann surfaces. The research delineates the intricate relationships between these rings, proving the P = W conjecture, and offering new insights into the structure of cohomology related to punctured spheres.
The Basics: What Are Character Varieties?
Character varieties arise naturally in the context of differential equations. Essentially, they represent equivalence classes of representations of the fundamental group of a surface, where these representations characterize how loops around 'punctures' affect solutions to linear ordinary differential equations. In simpler terms, think of a character variety as a way to classify different "behaviors" of solutions as they circle around certain critical points (the punctures).
Exploring the Fricke-Klein Example
An illustrative example provided by Mellit involves the computation of cohomology rings linked to a set of matrices associated with four specific parameters. This situation reveals deep connections to equations known as the Markov equations, which govern the parameters of these matrices. Through exhaustive calculations, Mellit shows that not only can we classify these matrices, but we can understand their collective behavior—essentially connecting algebraic properties to geometric insights.
New Developments: The P = W Conjecture
One of the most compelling revelations in Mellit's research is the proof of the P = W conjecture. This theorem postulates a relationship between the perverse filtration (P) and the weight filtration (W) in the context of cohomology rings. By establishing this connection, Mellit not only affirms existing theories but also paves the way for new methods of investigation in the field of algebraic geometry.
Implications for Mathematical Physics
These findings resonate beyond pure mathematics; they offer substantial implications for mathematical physics. The study elucidates how mathematical structures can intertwine with physical theories, particularly in areas such as gauge theory and string theory, where understanding character varieties can lead to insights into particle interactions and geometrical phase spaces.
Conclusion: A Step Forward in Algebraic Geometry
In conclusion, Mellit's work on the cohomology rings of character varieties represents a significant leap forward in understanding the intersection of algebra and geometry. His innovative approaches to the traditional theories add a rich layer of depth to our comprehension of these complex systems, inviting further exploration and application in both mathematics and physics.